Cuire un oeuf d’autruche à la coque.

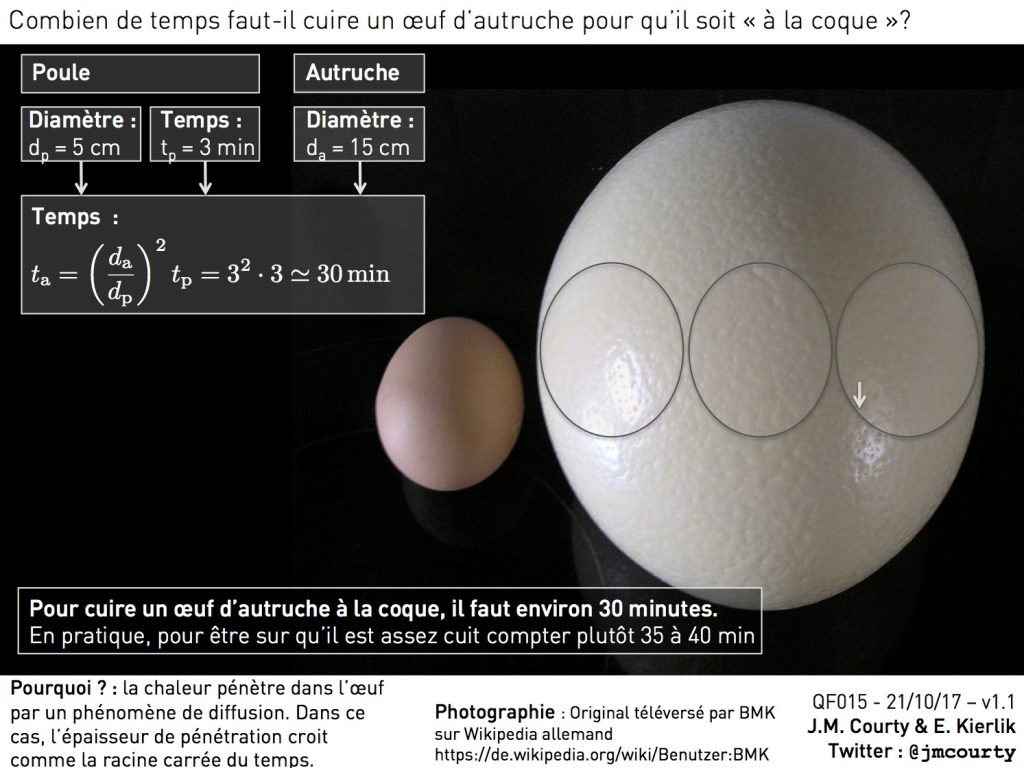
Pour cuire un oeuf d’autruche à la coque, compter une bonne demi-heure.

 

De quelles informations disposons nous ?

Pour cuire un oeuf de poule moyen à la coque, il faut compter 3 minutes de cuisson (en plaçant l’oeuf dans de l’eau bouillante).

En plus ce cette information, nous connaissons le diamètre d’un oeuf de poule : 5 centimètres environ et nous pouvons estimer ou trouver le diamètre d’un oeuf d’autruche : 15 centimètres.

En outre, la structure interne de ces oeufs est globalement la même. Nous pouvons donc considérer qu’ils sont homothétiques.

La question qui se pose est donc une loi d’échelle : si je multiplie la taille d’un oeuf par 3, par combien dois-je multiplier le temps de cuisson ? Le phénomène en jeu dans cette situation est la diffusion de la chaleur. Or le phénomène de diffusion est caractérisé par la loi d’échelle suivante : l’épaisseur chauffée croit comme la racine carrée du temps passé. Autrement dit, le temps nécessaire pour chauffer sur une certaine épaisseur est proportionnel à l’épaisseur au carré. Dans notre cas, l’épaisseur de blanc à cuire est 3 fois plus importante avec l’oeuf d’autruche qu’avec l’oeuf de poule. La durée de la cuisson sera donc 9 fois plus grande. Nous trouvons alors 27 minutes.

Comparaison avec les temps conseillés.

Les temps conseillés sur divers sites de cuisines sont bien de l’ordre de la demi-heure, mais ils sont systématiquement supérieurs. Les valeurs conseillées vont de 35 minutes à 45 minutes. Peut on expliquer ce désaccord ? Deux hypothèses viennent à l’esprit.

Tout d’abord, on pourrait penser à un effet de la coquille de l’oeuf d’autruche est épaisse de 2 à 3 millimètres, c’est à dire plus de 3 fois plus épaisse que celle d’un oeuf de poule. Il faut toutefois comparer les diffusivités thermiques : 0,143  mm²/s pour l’eau et 1,15 mm²/s pour le grès (c’est ce que j’ai trouvé de plus proche). (Source : https://en.wikipedia.org/wiki/Thermal_diffusivity ) autrement dit, la chaleur diffuse plus vite dans la coquille que dans le blanc. Ce n’est donc pas la bonne hypothèse.

Ensuite, il y a la taille de l’oeuf par rapport à la quantité d’eau qui sert à le cuire. Quand on cuit un oeuf de poule, le volume de l’oeuf est bien plus faible que le volume d’eau dans lequel on le place. Le refroidissement de l’eau dû au transfert de chaleur vers l’oeuf est donc faible et l’on peut considérer que l’eau reste en permanence à 100°C. Ce n’est pas le cas pour l’oeuf d’autruche avec une masse de plus d’un kilogramme et demi, l’effet sur la température de l’eau de cuisson n’est surement plus négligeable et cet effet allonge nécessairement le temps de cuisson. Est-il suffisant pour expliquer les 5 à 10 minutes supplémentaires ? Je ne le sais pas et j’invite les lecteurs à me faire part de leurs estimations ou de leurs expériences (mesurer la température de l’eau en faisant cuire un oeuf d’autruche).

La loi d’échelle sur la diffusion de la chaleur.

La diffusion de la chaleur dans un matériau est caractérisé par sa diffusivité thermique \( \alpha  \) qui est le rapport de la conductivité thermique \( k \) divisée par le produit de la masse volumique \( \rho \) et de la capacité calorifique \( c_{\rm{p}}  \) : \( \alpha = \frac{k}{\rho c_{\rm{p}}}  \).

La diffusivité thermique se mesure en m²/s . Cette unité est un premier moyen de trouver la loi d’échelle : pour conserver la diffusivité constante, il faut que le temps soit le carré de la taille typique.

On peut être plus précis à l’aide de l’équation de diffusion que j’écris à une dimension pour que les choses soient bien claires :

\( \frac {\partial }{\partial t} T=\alpha\frac {\partial^{2} }{\partial x^{2}} T \)

Cette équation est invariante si l’on effectue un changement de variables qui a pour effet de dilater en même temps les distances d’un coefficient  \(  \lambda \) et le temps d’un coefficient \(  \lambda^2 \).

Donc si l’on multiplie le diamètre de l’oeuf d’un coefficient donné, il faudra multiplier le temps par le carré de ce coefficient.

Détermination expérimentale de la loi d’échelle

On peut aussi chercher cette loi en analysant les temps de cuisson donnés pour des oeufs de différentes taille allant de la caille à l’autruche.

Les temps de cuisson viennent de ce site https://www.bbcgoodfood.com/howto/guide/ultimate-guide-eggs sauf pour l’autruche car dans la plupart des autres sites c’est bien moins que 50 minutes.

La taille des oeufs provient de ce site https://morningchores.com/duck-eggs/

Nous avons les valeurs pour les oeufs de caille, de poule, d’oie et d’autruche.

Nous cherchons donc une relation de la forme d’une loi de puissance \( t =a /, d^\beta  \)
où \( \beta \) est un exposant à déterminer. En pratique, il n’est pas aisé d’analyser graphiquement des lois de puissance, et il est bien plus simple d’étudier des relations linéaires. Pour cette raison, la recherche de lois d’échelles se fait usuellement en utilisant des échelles log-log. Autrement dit au lieu de chercher une relation entre la masse de la cloche et son diamètre, nous recherchons une relation entre les logarithmes de ces quantités. La relation attendue, en prenant le logarithme de la loi de puissance est alors \( \log t =\log a +\beta\log d \) . La relation est linéaire et la pente de la droite donne la valeur de l’exposant cherché.

Si vous le souhaitez, à vous de jouer avec les données pour trouver l’exposant grâce au tableur en ligne qui suit.  Les données ont été intégrées dans un tableur : elles sont représentées sur deux graphes en bleu. Le premier représente le temps de cuisson en fonction du diamètre de l’oeuf, le second, les logarithmes de ces quantités. En log-log, les données sont quasiment alignées. En rouge sont représentées les valeurs de la masse calculées à partir d’une loi de puissance dont l’exposant peut être changé à volonté. Pour cela, cliquez sur « click to edit » puis changez la valeur de l’exposant (qui a comme valeur initiale 2,2). En entrant une valeur et en tapant ensuite entrée, les valeurs sont recalculées et les nouvelles courbes tracées.

Nous pouvons vérifier que l’exposant  \( \beta =  2  \) donne le meilleur ajustement. Ce qui confirme l’hypothèse que nous avions fait sur le fait que le phénomène dominant est la diffusion de la chaleur. Il reste toutefois une interrogation sur le léger écart pour l’oeuf d’autruche.